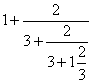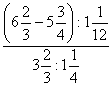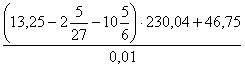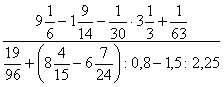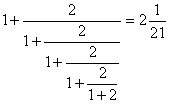Zestawy zadań z matematyki   I   Godzina wychowawcza   I   Problem narkotyków w szkole   I   Konkursy 
Ciekawe linki   I   Karta osiągnięć ucznia - ocena opisowa  I  Scenariusze zajęć   I  Osnowa lekcji gimnastyki korekcyjnej    I  Scenariusz "Dnia Matki"  I  Problem edukacyjny  I  Program edukacji regionalnej  I  Program edukacji zdrowotnej  I  Scenariusze uroczystości  I  Żywioły - scenariusze zajęć  I
Konkurs ortograficzny dla kl. III  I  Scenariusz międzyklasowgo turnieju

 

Zestawy zadań z matematyki

Test wielokrotnego wyboru   I   Zestaw zadań na konkursy matematyczne dla szkół podstawowych
Zestaw zadań na konkursy matematyczne dla klas gimnazjalnych

Test wielokrotnego wyboru

1.  Każda liczba dodatnia parzysta może być przedstawiona w postaci:

          A) 2n+2               B) 4n+2                C) n2+2                D)2n+1

2.      Liczba 0,1(6) jest liczbą:         

         A) wymierną  B) równą      C) większą od  D) niewymierną.

3.      Liczba 0,2222......  jest liczbą

         A) wymierną  B) równą     C) mniejszą od  D) niewymierną.

4. Odkurzacz  kosztował 200 zł, dodatkowe wyposażenie 50 zł. W ciągu roku odkurzacz podrożał o 30%, dodatkowe wyposażenie o 50%. W tej sytuacji całość zdrożała o:

          A) 85 zł.               B) 40%                 C) 34%                D) mniej niż 40%

5.      Pewna klasa ma 32 lekcje tygodniowo, codziennie nie mniej niż 4 i nie więcej niż 7 lekcji. W planie zajęć tej klasy musi być taki dzień, w którym lekcji jest dokładnie:

A) 7                     B) 6                      C) 5                     D) mniej niż 7. 

6.      Dana jest liczba a = 989,536. Jej przybliżenie

  A) do setek wynosi 1000                     B) do części setnych wynosi 989,5
  C) do jedności wynosi 990                  D) do części dziesiątych wynosi 98

7.      Konferencja przewidziana na 2 godziny przedłużyła się o 35% planowanego czasu. Trwała więc:

          A) 162 min         B) 9720 s            C) 2h 32min        D) nie więcej niż 3 godziny.

8.      4500 kg to:

          A) 4,5 ∙ 106 g        B) 4,5 ∙ 100 t         C) 4,5 ∙ 105 dag    D) 4,5 ∙109 mg

9.      Liczba 4 jest wynikiem działania

          A) ∙ B) C) D) 0,072 : 0,18

10.  W każdym rombie:
         A)    przekątne są dwusiecznymi kątów
         B)     punkt przecięcia przekątnych jest środkiem symetrii
         C)    suma kątów wewnętrznych przyległych do tego samego boku wynosi 1800.
         D)    P = a2  

11.  W każdym równoległoboku 
      A)    są dwie pary boków równoległych
      B)     4 osie symetrii
      C)    przeciwległe kąty równe 
      D)    przekątne przecinają się w połowie.

12.  Trójkąt równoramienny
      A)    może być trójkątem prostokątnym                           B) ma trzy osie symetrii
      B)     ma podstawę zawsze dłuższą od ramion                  C) ma środek symetrii.

13.  W każdym trójkącie prostokątnym
       A)    każdy bok ma inną długość
       B)     suma miar kątów ostrych wynosi 900
       C)    bok leżący naprzeciw kąta prostego jest najkrótszy
       D)    bok leżący naprzeciw kąta prostego to przeciwprostokątna.

14.  Dany jest kwadrat o wierzchołkach A = (3, 3); B = (-3, 3); C = (-3,-3); D = (3,-3), którego

          A) P = 36 j2          B) środkiem symetrii jest punkt 0 = (0,0)
          C) L = 36 j           D) oś X i Y to wszystkie jego osie symetrii.

15.  Pole działki w kształcie prostokąta o wymiarach 400m x 90m wynosi

          A) 3600 arów       B) 3,6 ha              C) 3,6 x 108 cm2   D) 36000 m2.

16.  Jeżeli α jest kątem środkowym, a β jest kątem wpisanym to:

          A) α = 2β             B) α = 900 i oparty jest na połowie okręgu
          C) β = 0,25α        D) β = 900 i oparty jest na połowie okręgu.

17.  Dany jest punkt M = (-2, 5)

    A) B = (2, -5) jest punktem symetrycznym względem początku układu współrzędnych
    B) A = (2, 5) jest punktem symetrycznym względem osi X
    C) C = (-2, -5) jest punktem symetrycznym względem osi X
    E)   D =(2, 5) jest punktem symetrycznym względem osi Y.

18.  Pan Jurek jest teraz 3 razy starszy od syna, a 10 lat temu syn był 7 razy młodszy od ojca.

      A)  pan Jurek i jego syn mają razem 60 lat
B)  syn jest obecnie uczniem gimnazjum
C)  za 15 lat ojciec będzie 2 razy starszy od syna
D)  pan Jurek jest o 30 lat starszy od syna.

19. 19.Trójkąt równoboczny można pociąć na:

      A)  4 trójkąty równoboczne
B)  3 trójkąty przystające
C)  3 czworokąty przystające
D)  trapez równoramienny i trójkąt równoboczny.

20.  20.Liczby a i b są parzyste i spełniają warunek a ∙ b = 1000. Wówczas:

      A)  jedna z tych liczb dzieli się przez 25
B)  jedna z tych liczb dzieli się przez 10
C)  żadna z tych liczb nie dzieli się przez 8
D)  żadna z tych liczb nie dzieli się przez 4.

21.  Dany jest trapez

      A)  zawsze można na nim opisać okrąg
B)  jeśli jest równoramienny, to można na nim opisać okrąg
C)  nigdy nie można na nim opisać okręgu
D)  jeśli można na nim opisać okrąg, to jest to trapez równoramienny.

22.  Śrubokręt i młotek kosztują tyle samo. Jeśli śrubokręt podrożeje o 5%, a młotek o 3%, to za zestaw 3 śrubokrętów i 3 młotków trzeba będzie zapłacić:

              A) o 4% więcej                            B) o 8% więcej
              C) o 15% więcej                          D) o 24% więcej.

23.  Mamy do dyspozycji dwa naczynia o pojemności 3 litry i 5 litrów. Posługując się nimi jesteśmy w stanie odmierzyć dokładnie:

          A) 1 litr                 B) 2 litry               C) 4 litry               D) 8 litrów.

24.  Wielościan ma dokładnie 6 krawędzi. Wynika stąd, że jest on:

          A) ostrosłupem                                  B) czworościanem
          C) sześcianem                                   D) czworościanem foremnym.

25.  Długości boków trójkąta równobocznego powiększono o 20%. Wynika stąd, że pole tego trójkąta wzrosło o:

          A) dokładnie 20%                             B) dokładnie 44%
          C) mniej niż 60%                               D) więcej niż 20%

26.  Cztery proste mogą podzielić płaszczyznę na dokładnie:

          A) 5 części           B) 8 części            C) 9 części           D) 12 części.

27.  Czworościan foremny i sześcian mają równe pola powierzchni. Zatem

      A)  krawędź sześcianu jest dłuższa od krawędzi czworościanu
B)  krawędź czworościanu jest dłuższa od krawędzi sześcianu
C)  krawędzie obu wielościanów są równe
D)  Sumy długości krawędzi obu wielościanów są równe.

28.  Przekątne:

      A)  w każdym kwadracie przecinają się pod kątem prostym
B)  w każdym prostokącie przecinają się pod kątem prostym
C)  w każdym rombie przecinają się pod kątem prostym
D)  w każdym rombie są równej długości.

29.  Liczba 0,(4) jest liczbą:

       A) niewymierną  B) mniejszą od   C) większą od D) równą  

30.  Przekrój sześcianu płaszczyzną może być:

          A) prostokątem                                 B) trójkątem równobocznym
          C) pięciokątem                                  D) trapezem równoramiennym.

31. Wśród liczb od 1 do 300 (włącznie) jest:

      A)  150 liczb podzielnych przez 2
B)  100 liczb podzielnych przez 3
C)  250 liczb podzielnych przez 2 lub 3
D)  50 liczb podzielnych przez 2 i 3 równocześnie.

32.  W klasie jest 10 dziewcząt i 20 chłopców.

         A) chłopcy stanowią   klasy
         B)   dziewczęta stanowią połowę klasy
         C)  chłopców jest dwa razy więcej niż dziewcząt
         D)  dziewcząt jest o 10 mniej niż chłopców.

 

33.   Marek przesypia doby wówczas śpi:

          A)9 godzin            B) 8 godzin           C) 540 minut        D) 32400 sekund.

34.  Książka ma 240 stron. Magda przeczytała 180 stron tej książki.

      A)  zostało jej do przeczytania 0,25 książki
B)  przeczytała już 0,75 książki
C)  zostało do przeczytania 80 stron
D)  przeczytała 3 razy więcej stron niż zostało jej do przeczytania.

35.  Które zdanie jest prawdziwe:

      A)  każdy kwadrat jest rombem
B)  każdy prostokąt jest kwadratem
C)  nie wszystkie równoległoboki są prostokątami
D)  istnieją równoległoboki , które są prostokątami?

36.  Dany jest ułamek

      A)  szóstą cyfrą po przecinku w jego rozwinięciu dziesiętnym jest 7
B)  jedenastą cyfrą po przecinku w jego rozwinięciu dziesiętnym jest 5
C)  rozwinięcie dziesiętne tego ułamka jest nieskończone okresowe
D)  na setnym miejscu po przecinku jest cyfra 8.

37.  Kij ma dwa końce.

      A)  półtora kija ma trzy końce
B)  dwa kije mają cztery końce
C)  dwa i pół kija mają pięć końców
D)  trzy kije mają sześć końców.

38.  Czy wszystkie romby o boku 1 mają jednakowe:

          A) pola                 B) sumę długości przekątnych
          C) obwody           D) sumę długości kwadratów przekątnych.

39.  Czy podana równość jest prawdziwa?

          A) B)
          C)  D)

40.  Które zdanie jest fałszywe?

      A)  wielokąt ma tyle kątów co boków
B)  trójkąt nie jest wielokątem
C)  bokami wielokąta są odcinki
D)  każdy wielokąt ma przekątne.

41.  Czy podana równość jest prawdziwa?

          A) MXCIX = 1099                           B) MMCML = 295
          C) CDIX = 4110                              D) DCX = 610

42.  Czy podane nierówności są prawdziwe?

          A) 15,16 1,527             B) 230,5< 230,09
          C) 19,50 > 19,5               D) 100,1 > 100,01

43.  Które zdanie jest prawdziwe?

      A)  wszystkie krawędzie sześcianu są równej długości
B)  wszystkie ściany sześcianu są przystające
C)  podstawą sześcianu jest sześciokąt foremny
D)  każda ściana sześcianu może być jego podstawą.

44.  Ułamek skraca się przez:

          A) 4                     B) 5                      C) 9                     D) 20

45.  Czy podane liczby są liczbami wymiernymi?

          A)                         B) 

          C)                        D)

46.  Czy liczba 72 + 1 jest podzielna przez:

          A) 2                     B) 3                      C) 5                     D) 10 ?

47.  Jeżeli dane są punkty A = (3,0), B = (7,0), C = (5,2), to 

      A)  trójkąt ABC jest prostokątny
B)  pole trójkąta wynosi 8
C)  obwód trójkąta ABC wynosi
E)   długość boku AB wynosi 4j

48.  Niech a = 610 i b = 185. Czy wtedy?

          A)                                    B)
          C)                                      D)

49.  W trapezie ABCD  wiadomo, że AD = BC i AB II DC. Które zdanie jest prawdziwe? 

            D              C   A) P = 12
B) Ð DAB = Ð ABC
C) L = 14
D)  Ð DAB + Ð BCD = 180 0

  A                                  B 

 

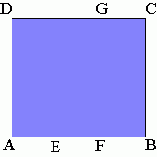
50.  W kwadracie ABCD punkty E i F leżą na boku AB, zaś punkt G na boku CD,

      przy czym AE = FB = CG = W takim razie:

A) Ð GFC = Ð GEC
B) Ð FCB = Ð EGF
C) Ð GEF = Ð GCF
D) Ð ECF = Ð FCB

 

51. Liczbą niewymierną jest: 

       A)                    B) P                        C)                      D) 48,2

52.  Dwa boki trójkąta mają długość 7cm i 8cm.Trzeci bok może mieć długość:

       A) 15cm                 B) 2cm                    C) 5cm                       D) 16cm

53.  Liczba 245a  jest podzielna przez 4, gdy w miejsce a wpiszemy cyfrę:

A) 4                         B) 2                         C) 0                          D) 6

54.  Liczba 12600000000 jest równa:

    A)         B)              C)             D)

55.  Która równość jest prawdziwa:

 A) DCDX = 1110                     B) MCDXC = 1490            
 C)CCCDC = 900                     D) MIM = 1999

56.  56. Ponumerowano 371 stron książki

      A)    w rzędzie jedności cyfra 3 występuje 37 razy
B)     w rzędzie dziesiątek cyfra 3 występuje 35 razy
C)    cyfra 3 występuje dokładnie 2 razy na 16 stronach
D)    cyfra 3 występuje ogółem 500 razy.

57.  W iloczynie

             A)    cyfra setek jest większa od cyfry jedności
      B)     cyfra dziesiątek jest równa 1
      C)    suma cyfry tysięcy i dziesiątek jest równa 5
      D)    występuje 6 cyfr.

58.  58.Jeżeli dane są trzy liczby 6, 15, 24 to:

     A) ich średnia arytmetyczna jest równa 25
     B)  pierwsza stanowi 0,4 drugiej
     C) pierwsza stanowi 20% drugiej
     D) druga stanowi trzeciej liczby.

    

59.  59.Jeżeli kwadrat ma pole 56cm2, to:

      A)    długość boku kwadratu jest większa od 7cm
B)     długość przekątnej jest mniejsza od 28cm
C)    długość boku kwadratu jest mniejsza od 8cm
D)    obwód kwadratu jest równy 64cm.

60.    Które twierdzenia są  prawdziwe

     A)  suma dwóch liczb ujemnych jest zawsze liczbą ujemną
B)     suma liczby ujemnej i liczby dodatniej jest zawsze liczbą dodatnią
C)    suma liczby ujemnej i liczby dodatniej jest zawsze liczbą ujemną
D)    suma liczby ujemnej i dwóch liczb dodatnich jest zawsze liczbą dodatnią.

61. Na okręgu opisano kwadrat i wpisano w niego kwadrat

      A)   pole kwadratu opisanego na okręgu jest większe od pola kwadratu
      wpisanego w okrąg
B)     pole okręgu jest mniejsze od pola kwadratu wpisanego w ten okrąg 
C)    otrzymana figura ma 4 osie symetrii
D)    długość promienia okręgu jest połową długości boku kwadratu wpisanego w
      okrąg.

62.  62. W pięciokącie foremnym:

      A)    kąt wewnętrzny ma miarę 1080
B)     można narysować 5 przekątnych
C)    można narysować 3 osie symetrii
D)    każdy bok ma inną długość.

63.  Liczba równa się

  

          A) 2002                B) 101101                  C) 110101                 D) 100111

64.  64.W trójkącie równobocznym:

      A)  wysokości dzielą się w stosunku 1 : 2
      B)  promień okręgu wpisanego jest wysokości
      C) kąty przy podstawie mają tę samą miarę
      D)  wysokość jest równa połowie boku.

 

65.  65. W równoległoboku:

      A)    suma kątów przeciwległych jest równa 1800
B)     punkt przecięcia przekątnych jest środkiem symetrii
C)    kąty przeciwległe są równe
D)    suma dwóch kolejnych kątów jest kątem rozwartym.

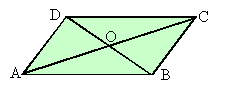
66.  66. Na rysunku punkt O jest środkiem okręgu 

      A) kąt a ma 1800

      B)    trójkąt ABC jest trójkątem prostokątnym
      C)  odcinek AC jest promieniem okręgu
      D) kąt a jest kątem środkowym.


67.  67. Który rok miał 366 dni

          A) 1607                     B) 1648                    C) 1700                     D) 1900?

68.  68. Akwarium o wymiarach 60cm, 40cm, 30cm można:

      A)    napełnić 72 litrami wody                                   C) napełnić 720 litrami wody
B)     wykonać z 0,8m2 szkła                                     D) wykonać z 0,9m2 szkła.

69. Ania kupiła  kg jabłek po 6zł i 5kg ziemniaków po 0,75zł za kilogram

          A)    zapłaciła za wszystko 9,25zł
   B)     jabłka kosztowały o 1zł mniej od ziemniaków
   C)    ziemniaki kosztowały o 25gr. więcej od jabłek
   D)    1kg jabłek jest 8 razy droższy niż1kg ziemniaków.

70. Rozwiązaniem równania jest :
       A) B)
       C) D)

 

71. Liczbą pierwszą jest :

          A) 485                        B) 433                      C) 927                        D) 929

72.  72. Liczba 1012 to :

          A) biliard                 B) bilion           C)1000miliardów                   D) 10003

73.  73. Pojazd A jechał z prędkością 72km/h, a pojazd B z prędkością 20m/s

      A)    pojazd A jechał z większą prędkością niż pojazd B
B)     pojazdy A i B jechały z tą samą prędkością
C)    pojazd A jechał z mniejszą prędkością niż pojazd B
D)    20m/s to inaczej 1200m/min.

74.  74.  Agata ma w swojej biblioteczce 15 książek, a Jacek 8 książek w tym 3 książki inne niż Agata. Ile ma Agata takich książek, których nie ma Jacek?

          A) 12 książek           B) 10 książek             C) 7 książek           D) 5 książek

75.  75. 10 kwintali to:

          A) 0,1t                      B) 1000kg                C) 10 000dag            D) 106g.

76.  76. Jest godzina 1400. Janek zabiera się do odrabiania lekcji. W czasie kiedy przygotowywał zeszyty i książki duża wskazówka zegara przesunęła się o kąt 600. Zadania z matematyki zajęły Jankowi 0,4 godziny, a ćwiczenia z gramatyki 2 kwadranse.

      A)    Janek był zajęty przez ponad 1 godzinę
B)     Janek skończył ćwiczenia z gramatyki o godzinie 1505
C)    Janek był zajęty przez 64 minuty
D)    Jankowi więcej czasu zajęła matematyka niż ćwiczenia z gramatyki.

77.  77. Dany jest kwadrat o polu 64cm2 i prostokąt, którego jeden bok jest dwa razy dłuższy niż bok kwadratu, a drugi bok dwa razy krótszy niż bok kwadratu.

      A)    obwód prostokąta jest większy niż obwód kwadratu o 8cm
B)     pola obu figur są równe
C)    obwody obu figur są równe
D)    bok kwadratu ma 8cm długości.

78.  Dany jest ułamek właściwy o postaci  , w którym n + k = 20

                  A)    takich ułamków jest 10
   B)     są 4 takie ułamki nieskracalne
   C)    wszystkie takie ułamki są nieskracalne
   D)    suma liczników i mianowników wszystkich ułamków wynosi 180.

79.  79. Matka rozdzieliła 29 zł kieszonkowego na trzech synów. Najstarszy otrzymał o  4 zł więcej od średniego, a ten o2 zł więcej od najstarszego.

      A)    najmłodszy syn otrzymał o 4 zł więcej od najstarszego
B)     najmłodszy i najstarszy syn mieli razem 20 zł
C)    najmłodszy i średni syn mieli razem więcej niż najstarszy syn
D)    najstarszy syn otrzymał od matki 13 zł.

80.  80. Dana jest liczba czterocyfrowa parzysta podzielna przez 3

      A)    najmniejsza taka liczba to 1112
B)     najmniejsza taka liczba dzieli się przez 5
C)    największa taka liczba to 9996
D)    największa taka liczba to 9999.

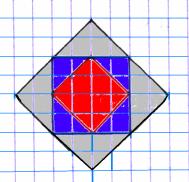
81.  81. Narysowane kwadraty: najmniejszy (1), średni (2) i największy (3) mają rzeczywiste wymiary (jak na rysunku)

A)  suma pól wszystkich kwadratów

        wynosi 14cm2 

B)  pole kwadratu (3) jest cztery razy

    większe od pola kwadratu (1)

C)  obwód kwadratu (2) ma 8cm długości

     D)suma pól kwadratów (1) i (2)  jest

         większa niż pole kwadratu (3).

 
82. Dane są następujące wielkości: a =  tuzina, b =  mendla, c = kop

        A) a  < b i b = c         B) a < b i b > c          C) a + b + c =29            D) b = 8

83.  83. Dane są następujące wielokąty:

A)    jedną oś symetrii mają trzy figury

B)     kwadrat ma cztery osie symetrii

C)    trójkąt ma jedną oś symetrii

D)    równoległobok nie ma osi symetrii.

84. Jeżeli a, b, c są liczbami naturalnymi większymi od zera takimi, że a > b > c, to:

          A) a + b > a + c                                            B) a – b > a – c

          C) a × b > a × c                                               D) a : b > a : c

85. Dane są następujące wyrażenia: 

      a = 0,01 : 100,  b = 0,00001 ×10,  c = 10: 1000000,  d = 0,01 × 0,01

A)    największą wartość ma wyrażenie d

B)     najmniejszą wartość ma wyrażenie a

C)    wyrażenia a i d mają równą wartość wynoszącą 0,001

D)    wszystkie wyrażenia mają równą wartość.

86. 2 cegły ważą 3kg i pół cegły

A)    jedna cegła waży 1,5kg

B)     jedna cegła waży 2kg

C)    500 takich cegieł waży 1 tonę

D)    nie można obliczyć ile waży 1 cegła.

87. Długości boków trójkąta są liczbami mniejszymi od 5

A)    takich trójkątów jest 13

B)     takich trójkątów jest 15

C)    trójkąt o bokach 3, 3, 3 nie odpowiada warunkom zadania

D)    trójkąta o bokach 1, 2, 3 nie da się zbudować.

88. Dane są liczby: 1, 2, 3 i 4

A)    suma kwadratów wszystkich tych liczb równa się 30

B)     kwadrat sumy wszystkich tych liczb równa się 102

C)    średnia arytmetyczna tych liczb wynosi 2,5

D)    iloczyn tych liczb wynosi 24.

89. Zegar wskazuje godzinę 1500. Od tego czasu duża wskazówka zegara 

       wykonała 305 pełnych obrotów

A) obecnie zegar wskazuje godzinę1505

B)     obecnie zegar wskazuje godzinę 2000

C)    na wykonanie wszystkich obrotów potrzebowała duża wskazówka ponad 12 dni kalendarzowych

D)    w wyżej wymienionym czasie mała wskazówka wykonała 13 pełnych obrotów.

90.  90. Ile trójkątów widać na rysunku?

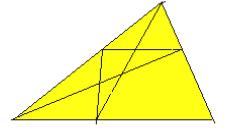A)    więcej niż 19
B)     mniej niż 20
C)    19
D)    20.

 

91.  91. W sklepie są jabłka po 1,50zł za kilogram i 2zł za kilogram.

 Klientka X kupiła 2kg jabłek droższych i 3kg jabłek tańszych.

 Klientka Y kupiła 3kg jabłek droższych i 2kg jabłek tańszych.

A)    obie klientki zapłaciły równe kwoty za kupione jabłka

B)     klientka X zapłaciła o 50gr mniej niż klientka Y

C)    1kg mieszaniny jabłek klientki X kosztował 1zł 80gr

D)    1kg mieszaniny jabłek klientki Y kosztował 1zł 90gr.

92.  92. Dwie proste na płaszczyźnie

A)    nie mają punktów wspólnych

B)     mają jeden punkt wspólny

C)    przecinają się pod kątem prostym

D)    mają wszystkie punkty wspólne.

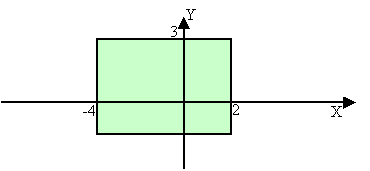
93.  93. Wierzchołki prostokąta mają współrzędne A=(0,-2), B=(5,-2), C=(5,3), D=(0,3). Jakie warunki spełniają punkty należące do prostokąta ABCD?

          A) 0 < x < 5  i  –2 < y < 3                            B) –2 < x < 3  i  0 < y < 5

          C) 0 £ x £ 5  i  –2 £ y £ 3                            D) –2 £ x £ 3  i  0 £ y £ 5.

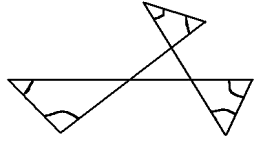
94.  94. Dwusieczne kątów przy podstawie trójkąta równoramiennego ABC przecinają się pod kątem 1300. Wówczas:

      A)    Kąt a ma miarę 1300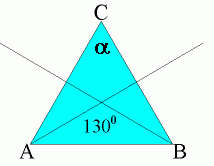  
      B)     Kąt a ma miarę 800
      C)    Kąty przy podstawie są równe i mają po 500  
      D)    Trójkąt ma 1 oś symetrii.   

                                                                           

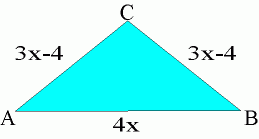
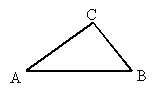
95.  95. Trójkąt ABC jest trójkątem równoramiennym, którego obwód wynosi 50j, wówczas:

      A)    podstawa AB = 23,2j

      B)     podstawa AB = 5,8j
      C)    ramiona są długości 13,4j  
      D)    ramiona są krótsze od podstawy.

             

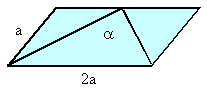
96.  96. Obwód rombu jest równy 16j, uwzględniając warunki podane na rysunku wiemy, że:

      A)  kąt a ma 960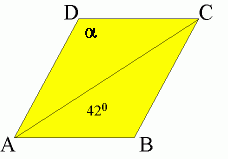 
      B) nie wiadomo jaką ma miarę kąt a –
           ponieważ mamy zbyt mało danych
      C)   kąt ostry rombu ma 840
      D)  przekątna AC dzieli romb na 2
           przystające trójkąty

   

97.  97. Przeciętny koń waży około 700kg, a przeciętny człowiek około70kg,czyli

A)    koń jest cięższy od człowieka o100%

B)     Koń jest cięższy od człowieka o 1000%

C)    waga człowieka to 10% wagi konia

D)    człowiek jest lżejszy od konia o mniej niż 90%.

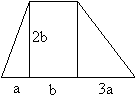
98.  98. Pole pewnego trapezu wynosi P, wówczas:

       A)  B)
       C)  D)

         

99.  99. Trójkąt prostokątny równoramienny ma ramię długości 4cm, wtedy:

       A)  przeciwprostokątna jest równa
       B) wysokości tego trójkąta wynoszą 
       C)   pole trójkąta wynosi
       D)  obwód trójkąta jest równy

    

100.    Dany jest okrąg o promieniu  i kwadrat opisany na tym okręgu
          A) bok tego kwadratu jest równy promieniowi okręgu
          B)  obwód kwadratu wynosi
                   C) pole kwadratu wynosi 
          D) pole figury ograniczonej między bokami kwadratu i okręgiem jest równe

        

 

Powrót

 

Zestaw zadań na konkursy matematyczne dla szkół podstawowych

 

1.      Pole prostokąta wynosi 22cm2. Długość tego prostokąta ma 5,5cm. Oblicz o ile pole kwadratu jest większe od pola prostokąta wiedząc, że figury te mają równe obwody.

2.      Oblicz wartość ułamka

3.      Jak przedstawić liczbę 31 pięcioma piątkami?

4.      Znajdź co najmniej 3 liczby pierwsze, które pomniejszone o 1 dają kwadrat liczby naturalnej.

5.      Na ile sposobów można rozmieścić nawiasy  w wyrażeniu 3:3:3:3. Ile przy tym można otrzymać różnych liczb?

6.      Wśród liczb od 1 do 1000 ile jest takich liczb, które dzielą się przez 4 i nie posiadają cyfry 4 w swoim zapisie?

7.      W koszu jest mniej niż 100 jabłek. Można je podzielić po równo ( nie krojąc) między 2 lub 3 lub 5 dzieci, ale nie można rozdzielić po równo między 4 dzieci. Ile jabłek jest w koszyku?

8.      Dowolny trójkąt podzielić dwoma prostymi cięciami na pięciokąt, czworokąt i dwa trójkąty.

9.      Ile można wykonać różnych trójkolorowych chorągiewek z 4 barw ( kolejność barw odgrywa rolę ).

10.  Wyznacz wartość x z równania

11.      Przeciętny człowiek śpi 8 godzin na dobę. Ile lat przespał przeciętny 60-letni człowiek.

12.      Przedstaw liczbę 452 w postaci iloczynu liczb pierwszych.

13.      Przez wierzchołek prostokąta poprowadź dwie proste tak, aby podzieliły go na trzy części o równych polach.

14.      Wymień trzy liczby niewymierne, które należą do rozwiązań nierówności 

15.      Udowodnić, że kąt ostry zawarty między przekątnymi prostokąta jest 2 razy większy od kąta, który tworzy przekątna z dłuższym bokiem.

16.      Jedna maszynistka pisze 16 wierszy w ciągu 5 minut, a druga 26 wierszy w ciągu 8 minut. Która z nich pisze prędzej?

17.      Dzieci grają w „chińczyka”. Mama funduje nagrodę w postaci tabliczki czekolady i mówi śmiejąc się: „Pierwszy otrzyma połowę, drugi jedną trzecią, a trzeci jedną czwartą tabliczki”. Dlaczego mama się śmiała?

18.      O ile różnica liczb i jest mniejsza od sumy tych liczb?

 

19.    Klasa V liczy 40 dzieci. Na półrocze dzieci otrzymały następujące oceny: liczby uczniów była z oceną
       bdb, z oceną db, z oceną dst i z oceną ndst.
       Czy każdy uczeń otrzymał ocenę?

20.  Zmieszano 5kg cukierków po 18,40zł za 1kg i 7kg po zł za 1kg. Jaka jest cena 1kg  mieszaniny?

21.      Wykonaj wskazane działania i oblicz 40 % wartości tego wyrażenia
22.   W miasteczku są trzy szkoły podstawowe. Do jednej z nich uczęszcza ogólnej liczby uczniów,
      a do drugiej 1,5 razy więcej. Ile procent ogółu uczniów uczęszcza do każdej z tych trzech szkół?

23.      Za 15m płótna zapłacono 185zł.  Ile trzeba zapłacić za 18m tego płótna?

24.    Najwyższy człowiek na świecie miał w wieku dojrzałym 2,8m, a najniższy 42cm wzrostu. Oblicz stosunek wzrostu człowieka najwyższego do najniższego.

25.    Oblicz długość boku trójkąta równobocznego wiedząc, że połowa obwodu tego trójkąta jest równa obwodowi kwadratu o boku 1,44m.

26.    Jacek pomyślał sobie pewną liczbę i pomnożył ją przez  6. Dzieląc 750 przez ten iloczyn otrzymał 50. Jaką liczbę pomyślał Jacek?

27.      Suma trzech liczb wynosi Pierwsza liczba jest większa od drugiej o , a od trzeciej o

Jakie to liczby?

28.   Skonstruuj trapez równoramienny, którego dłuższa podstawa jest równa średnicy okręgu, a długość ramienia jest równa długości promienia okręgu.

29.   W rombie miara kąta ostrego wynosi 600. Oblicz miary kątów wewnętrznych tego rombu.

30.  Zbuduj romb o przekątnych 6cm i 8cm.

31.  W trójkącie ABC dane są kąty Ða =800, Ðb =650. Oblicz miarę kąta zewnętrznego przy wierzchołku C.

32.  Długość krawędzi bocznej prostopadłościanu o podstawie kwadratowej jest równa 8dm.Oblicz sumę długości wszystkich krawędzi wiedząc, że krawędź podstawy jest dwa razy krótsza od długości krawędzi bocznej. Oblicz pole powierzchni tego prostopadłościanu oraz jego objętość.

33.  Oblicz wartość tego wyrażenia 

34.  W sadzie rośnie 60 drzew owocowych. wszystkich drzew to jabłonie, - orzechy włoskie,

wiśnie, a reszta to grusze.
      Ile grusz rośnie w sadzie?

 35.      Oblicz liczbę, której 25% wynosi:   

36.      Pole kwadratu wynosi 400dm2. Jeden bok kwadratu zmniejszono o 10%. Oblicz pole otrzymanego prostokąta. Ile procent pola kwadratu stanowi pole otrzymanego prostokąta?

37.      Znajdź długość krawędzi sześcianu mającego 2 razy większą objętość od objętości prostopadłościanu o krawędziach długości 5mm, 5cm i 2,5dm. Oblicz pole powierzchni całkowitej i sumę długości wszystkich krawędzi tego sześcianu.

38.      Ile liczb czterocyfrowych można zapisać za pomocą cyfr 0, 3, 5, 7?

39.    Pole prostokąta wynosi 28cm2.Długość tego prostokąta wynosi 5,5cm. Oblicz o ile pole tego kwadratu jest większe od pola prostokąta wiedząc, że figury te mają równe obwody.

40.   Między ułamkami  i wstaw taki ułamek, aby był większy od  a mniejszy od

41.   Jedna klientka kupiła 25m materiału, a druga 6m tego samego materiału. Pierwsza zapłaciła o 523zł więcej niż druga. Ile złotych kosztował 1m materiału?

42.   W mieście są trzy kina, w pierwszym kinie jest 400 miejsc, w drugim o 15% więcej niż w pierwszym, a w trzecim o 15% mniej niż w drugim. Ile miejsc jest w trzech kinach razem?

43.  Długość sali szkolnej w kształcie prostopadłościanu wynosi 12,5m, jej szerokość stanowi
      długości, a wysokość 0,8 szerokości. Oblicz objętość tej sali.
44.  Liczbę 1 przedstaw w postaci sumy trzech ułamków, których liczniki są równe 1.

45.  Uczeń przeczytał książkę w ciągu trzech dni. W pierwszym dniu przeczytał 0,2 książki jeszcze 16 stron, w drugim dniu 0,3 reszty i20 stron, w trzecim 0,75 tego co pozostało i ostatnie 30 stron. Ile stron ma ta książka?

46.  Bok kwadratu ma długość dm. O ile procent zwiększy się pole tego kwadratu, jeśli jego bok zwiększymy o 25%?
47.  Szerokość prostokątnego parku stanowi jego długości. Idąc z prędkością 5km/h można obejść park
     dookoła w ciągu 15 minut. Ile hektarów ma ten park?
48.  W drużynie harcerskiej chłopcy stanowią tej drużyny, a dziewcząt jest o 12 mniej niż chłopców.
      Ile dzieci jest w tej drużynie?

49.  Ile boków ma wielokąt wypukły, w którym suma kątów wewnętrznych wynosi 18000?

50.  Na chodnik do szkoły o szerokości 2 m zużyto 512 płytek kwadratowych o boku 0,3m.
     Ile metrów długości ma chodnik?
51.  Ania kupowała prezenty gwiazdkowe. W pierwszym sklepie wydała swoich oszczędności i jeszcze
     10zł, w drugim 0,2 reszty i jeszcze 20zł, a w trzecim ostatnie 2zł. Ile pieniędzy wydała Ania?

52.  Oblicz 72% liczby „a”, jeśli

   a =
53.  Wierzchołki trójkąta ABC należą do okręgu. Łuk, na którym opiera się kąt ABC jest 2 razy dłuższy od
      łuku, na którym opiera się kąt BAC i 1 razy dłuższy od łuku, na którym opiera się kąt ACB.
     Wyznacz miary kątów trójkąta ABC.

54.  Oblicz, ile blachy potrzeba na wykonanie otwartej puszki prostopadłościennej o wymiarach podstawy 6cm i 9cm oraz wysokości 12,5cm. Na spojenia dolicz 5% blachy.

55.   Jak mając do dyspozycji naczynia o pojemności 17 litrów i 5 litrów odmierzyć z cysterny 13 litrów wody?

56.  Wśród 15 monet jednakowych na wygląd jedna jest fałszywa (różniąca się od pozostałych ciężarem). Jak przy pomocy nie więcej niż 2 ważeń, na wadze szalkowej bez odważników, ustalić czy jest ona cięższa, czy lżejsza od pozostałych?

57.  W równoległoboku ABCD bok AB=9cm, przekątna BD=12cm, a wysokość poprowadzona z wierzchołka D na bok AB jest równa 4cm.Oblicz odległość punktu A od prostej BD.

58.  Prostokąt, którego kolejne boki mają długość 8cm i 18cm podzielić na dwie części tak, aby można z nich było złożyć kwadrat.

59.  Do liczby 403 z prawej i lewej strony dopisać po jednej cyfrze tak, aby liczba pięciocyfrowa dzieliła się przez 45.

60.  Prostokąt podzielono na dwa kwadraty o wspólnym boku. Oblicz pole tego prostokąta, jeżeli jego obwód wynosi 86,4cm.

61.  Podłoga sali ma kształt prostokąta o wymiarach 40,5m i 20,4m.Podłogę trzeba wyłożyć deskami o wymiarach 45cm i 35cm Ile potrzeba desek?

62.  Brygada kosiarzy w ciągu pierwszego dnia skosiła połowę łąki i jeszcze 2 hektary. Drugiego dnia skosiła 25% pozostałej łąki, przy czym pozostało jeszcze 6 hektarów do skoszenia. Jaka była powierzchnia łąki?

63.  Dane są ułamki i Znajdź taką największą liczbę, przy dzieleniu przez którą każdego z danych
      ułamków otrzymamy liczbę całkowitą.

64.  Znajdź odjemną i odjemnik SSSS - SSS = 2. Symbole „S” oznaczają cyfry. Ile rozwiązań ma zadanie?

65.  Trzech chłopców kupiło 14 ciastek. Andrzej kupił 2 razy mniej niż Jacek, a Marek kupił więcej niż Andrzej, ale mniej nią Jacek. Ile ciastek kupił każdy z chłopców?

66.  Na lekcji matematyki 12% uczniów nie rozwiązało w ogóle zadań, 32% uczniów rozwiązało te zadania z błędami, a reszta klasy w liczbie 14 uczniów rozwiązała te zadania bezbłędnie. Ilu uczniów było w klasie?

67.  Z miejscowości odległych o 140km wyjechali jednocześnie na spotkanie dwaj rowerzyści, z których jeden jechał z prędkością 17km/h, drugi 18km/h. Po ilu godzinach jazdy się spotkali?

68.  O ile procent zwiększył robotnik wydajność pracy, jeśli to co robił w ciągu 9 godzin, wykonał potem w ciągu 8 godzin?

69.  Czy można obrać na płaszczyźnie pięć różnych punktów w ten sposób, aby prowadząc prostą przez każde dwa z nich otrzymać dokładnie:

                        a)    1 prostą                  b)  2 proste                         c)  3 proste       

                        d )   4 proste                  e)  5 prostych                      f)  6 prostych?

70.  W kwadrat wrysowano mniejszy kwadrat w ten sposób, że wierzchołki mniejszego kwadratu są środkami boków większego kwadratu. Jaki ułamek pola jednego kwadratu stanowi pole kwadratu drugiego?

71.  Kąt A w trójkącie ABC jest większy od kąta B o 400, a kąt C jest o 100 większy od kąta A. Znajdź kąty tego trójkąta.

72.  Fabryka wyprodukowała 990 torebek przekraczając plan o 10%. O ile procent przekroczy plan, jeśli wyprodukuje 1000 torebek?

73.  W wyrażeniu  ustaw nawiasy w ten sposób, aby otrzymać:

      a)      liczbę 50
b)      liczbę możliwie najmniejszą
c)      liczbę możliwie największą.

74.  Przez wierzchołek kwadratu poprowadzono prostą, która dzieli kwadrat na trójkąt o polu równym 24 i trapez o polu 40.Oblicz długości podstaw trapezu.

75.  Jakie liczby ukryto pod znakami

                           s +  “  +  m +  m = 26
                           s +  s +  š  +  m = 22
                           s +  ?  +  ?  +  m = 24

76.  Na wycieczkę pojechało 28 uczniów, co stanowiło 87,5% wszystkich uczniów  w klasie. 50% liczby uczniów, którzy nie pojechali na wycieczkę stanowiły dziewczęta. Ile dziewcząt nie pojechało na wycieczkę?

77. Oblicz   

78.  Dany jest prostokąt, którego obwód wynosi 18cm. Wzdłuż jednego boku prostokąta odcięto pasek o szerokości 2cm, a wzdłuż drugiego o szerokości 1cm. Otrzymujemy kwadrat. Jakie były wymiary prostokąta?

79. Jak od kawałka długości m odciąć kawałek o długości 0,5m nie mając przy sobie linijki?

80.   Liczbę „a” zmniejszono o 15%, a następnie tak otrzymaną liczbę zwiększono o 15%. Czy otrzymana liczba jest większa, czy mniejsza od liczby „a”?

81.   Jeżeli między cyfry liczby dwucyfrowej wpisać 0, to otrzymana liczba trzycyfrowa będzie 9 razy większa od początkowej. Znaleźć tę liczbę.        

                                                                                                          Opracowała:
                                                                                                          mgr Jadwiga Wawrzyniak
                                                                                                          mgr Grażyna Musielak

Powrót

Zestaw zadań na konkursy matematyczne dla klas gimnazjalnych

1.      Wykaż, że kwadrat dowolnej liczby pierwszej większej od 3 przy dzieleniu przez 24 daje resztę 1.

2.      Ile wynosi iloraz z dzielenia liczby  109 + 108 + 107  przez 555?

3.      Suma dwóch liczb jest równa , a ich różnica

 . Udowodnij, że ich iloczyn jest równy 1.

4.      Wykaż, że suma dwóch kolejnych liczb nieparzystych jest podzielna przez 4.

5.      Wykaż, że suma czterech kolejnych liczb nieparzystych jest podzielna przez 8.

6.      Udowodnij następujące twierdzenie:

Jeżeli od liczby dwucyfrowej odejmiemy liczbę powstałą z przestawienia cyfr tej liczby, to otrzymamy liczbę podzielną przez 9.

7.    Udowodnij następujące twierdzenie:

Suma liczby dwucyfrowej i liczby powstałej z przestawienia jej cyfr jest liczbą podzielną przez 11.

8.    Uzasadnij, że dla każdej liczby naturalnej n liczba  n2 + n jest parzysta.

9.    Uzasadnij, że suma trzech kolejnych liczb naturalnych jest podzielna przez 3.

10.  Uzasadnij, że suma czterech kolejnych liczb naturalnych nie jest podzielna przez 4.

11.   Czy poniższa równość jest prawdziwa?    

   

12.  Które z podanych niżej ułamków przedstawiają liczby naturalne?

                                                                    

                                                                   

13. Podane liczby przedstaw w postaci różnych ułamków prostych (ułamki proste to takie, które mają licznik równy 1):

a)  b) c) d)

14.  Dwa samochody wyjechały jednocześnie z Warszawy do Radomia. Pierwszy samochód jechał połowę czasu podróży z prędkością 70km/h, a drugą połowę z prędkością 60km/h. Drugi samochód jechał pierwszą połowę drogi z prędkością 70km/h,  a drugą połowę z prędkością 60km/h. Który samochód szybciej dotarł do celu?

15.  Firma Mixmax kupiła 20kg rodzynek, 12kg migdałów oraz 14kg orzechów. Kilogram rodzynek kosztował 6,70zł, migdałów – 40zł, a orzechów-23,50zł. Bakalie wymieszana i zapakowano w woreczki po 200g do każdego. Jaka powinna być cena jednego woreczka bakalii, aby na każdym firma Mixmax zarobiła złotówkę?

16.  Kasia zbierała w skarbonce bilon. Po otwarciu okazało się, że miała w niej 45 dziesięciogroszówek, 60 dwudziestogroszówek i 27 pięćdziesięciogroszówek. Jaki procent wszystkich pieniędzy miała w pięćdziesięciogroszówkach?

17.  W zeszłym tygodniu na dyskotece szkolnej było tyle samo chłopców co dziewcząt. W tym tygodniu na dyskotece jest o 20% więcej osób niż tydzień temu, ale liczba dziewcząt stanowi tylko 45% liczby osób, które przyszły dzisiaj potańczyć. Czy w tym tygodniu przyszło więcej czy mniej dziewcząt niż tydzień temu?

18.  Oto zadanie ułożone przez Johna Mellisa w 1594 roku:

Jeśli 1 jard sukna kupujesz za 6 szylingów i 8 pensów, a sprzedajesz za 8 szylingów i 6 pensów, to ile zarobisz na każdych 100 funtach zainwestowanych w taką transakcję?

(W 1594 roku 12 pensów stanowiło równowartość 1 szylinga)

19.  Dwaj sprzedawcy, panowie A i B, kupują jabłka u tego samego hurtownika. W sklepie pana A cena detaliczna jest o 25% wyższa od hurtowej, a w sklepie pana B o 30% wyższa od hurtowej. Pan A sprzedał 160kg jabłek, a pan B – 120kg. Który z nich więcej zarobił na jabłkach? O ile procent więcej?

20.  Cenę towaru obniżono o 30%, a później jeszcze o 20%. O ile procent jest cena niższa w     porównaniu z pierwotną?

21.  Zmieszano pewną ilość kilogramów 40% roztworu soli z dwa razy większą ilością kilogramów 10% roztworu tej soli. Ile procentowy roztwór otrzymano?

22.  O ile procent zmniejszyłaby się dzienna produkcja, gdybyśmy chcieli bez zwiększania wydajności pracy przejść z ośmiogodzinnego dnia pracy na siedmiogodzinny? O ile procent należałoby zwiększyć wydajność pracy, aby dzienna produkcja nie uległa zmianie?

23.  Wczoraj w klasie uczniów obecnych było 8 razy tyle co nieobecnych. Dzisiaj nie przyszło jeszcze dwóch i teraz nieobecni stanowią 20% uczniów obecnych. Ilu jest uczniów w klasie?

24.  Po zmieszaniu 40% roztworu kwasu siarkowego z 60% roztworem tego kwasu i 5 litrami wody, otrzymano roztwór 20%. Gdyby zamiast 5 litrów wody dolano 5 litrów roztworu 80%, otrzymano by roztwór 70%. Ile było litrów roztworu 40%, a ile 60%?

25.  Cena biletu na mecz piłki nożnej wynosiła 15zł. Gdy cenę obniżono okazało się, że na mecz przychodziło o 50% widzów więcej, a dochód uzyskany ze sprzedaży biletów za jeden mecz wzrósł o 25%. O ile obniżono cenę biletu?

26.  Ile kilogramów roztworu osiemdziesięcioprocentowego należy zmieszać z 40 kilogramami roztworu sześćdziesięcioprocentowego, aby otrzymać roztwór siedemdziesięcioprocentowy?

27.  Stopiono dwa różne stopy cyny i ołowiu. Otrzymano 45,5kg stopu zawierającego 65 % cyny. 

      Ile kilogramów ważył pierwszy stop, jeśli stosunek wagowy cyny do ołowiu w pierwszym stopie 
wynosił 3 : 2, a w drugim 2 : 1?

28.  Z 1000kg rudy o zawartości 37,5% żelaza usunięto 400kg domieszek o zawartości 15% żelaza. O ile procent podniosła się zawartość żelaza w pozostałej bryle?

29.  W wyrażeniu  x2 – 1 – 2x2 + 7  wstaw nawiasy tak, aby niezależnie od wartości zmiennej x otrzymane wyrażenie miało wartość:

                                      a) ujemną                       b) dodatnią.

30.  Oblicz sprytnie wartość wyrażenia  x2 + 0,77x – 0,46  dla x = 1,23.

31.  Oblicz pole narysowanego trapezu, wiedząc, że 24ab + 12b2 = 13. 

32.  Średnia temperatura pierwszych dwunastu dni grudnia wyniosła 30 C, a pierwszych trzynastu dni grudnia 20 C. Jaką temperaturę zanotowano 13 grudnia?

33.  Oblicz ile lat ma autor tej wypowiedzi:

„4 lata temu byłem 4 razy młodszy od mamy, a 10 lat temu byłem od niej młodszy 10 razy”.

34.  Krzyś postanowił, że będzie czytał po 40 stron książki dziennie. Niestety, czytał tylko 30 stron dziennie i przeczytanie całej książki zabrało mu 3 dni więcej, niż planował. W ciągu ilu dni Krzyś przeczytał całą książkę? Ile stron liczyła owa lektura?

35.  Gdy pan N. A. Iwniak zaczynał grę z panem O. Szustem, miał tyle samo gotówki co on. Na początku wygrał 20zł, ale potem przegrał  dwie trzecie tego, co posiadał. W rezultacie miał cztery razy mniej pieniędzy niż O. Szust. Z jaką kwotą obaj panowie rozpoczynali grę?

36.  W liczbie trzycyfrowej suma cyfr setek i jedności wynosi 15. Jeżeli cyfry liczby poszukiwanej napiszesz w odwrotnej kolejności, to otrzymasz liczbę o 297 większą od poszukiwanej. Gdybyś zaś przed cyfrą setek liczby poszukiwanej dopisał 7, to nowo utworzona liczba czterocyfrowa byłaby o 1151 większa od liczby czterocyfrowej, jaką otrzymałbyś, dopisując na końcu liczby poszukiwanej cyfrę 8. Wyznacz liczbę poszukiwaną.

37.  Motocykl przebył 84km w ciągu 2 godzin i 24 minut. O ile należy zwiększyć prędkość, aby przebyć tę drogę w ciągu 2 godzin i 6 minut?

38.   Obwód czworokąta PRST jest pięć razy większy od długości przekątnej RT. Obwód trójkąta PRT jest równy 40, a obwód trójkąta RST jest równy 23. Jaką długość ma przekątna RT?

39.  Miejscowości A,B,C połączone są między sobą drogami tak jak na rysunku. Długość drogi od A do C przez B jest cztery razy większa od długości drogi od A do C. Długość drogi od B do A przez C jest o 5km większa niż długość drogi od B do A. Natomiast długość drogi od C do B przez A wynosi 85km. Oblicz długość drogi między każdą parą miejscowości.

40.  Obwód czworokąta wynosi 0,28m. Długość drugiego boku jest o 5cm większa od długości
   pierwszego. Długość trzeciego boku stanowi 75% długości drugiego boku, a długość czwartego boku jest

  równa  długości boku trzeciego. Oblicz długość każdego boku czworokąta.

41.  Irek ma w indeksie tylko piątki, czwórki i trójki. Trójek ma najwięcej, o 10 więcej niż    piątek. Czwórek ma trzy razy więcej niż piątek. Ile ma trójek, czwórek i piątek, jeśli średnia jego ocen jest niższa niż 3,6? 

42.  Dla jakie wartości a rozwiązaniem równania    jest liczba   „-2”? Dla jakiej wartości a równanie to nie ma rozwiązania? 

43.  Rozwiązać równania z niewiadomą x, w których litery a, k, m oznaczają parametry:

                   a)

                   b)

                   c)

                   d)

44.  Oblicz sumę miar wszystkich zaznaczonych kątów.


45.  Narysuj dowolny kąt a, dowolny odcinek a i dłuższy od niego odcinek h. Skonstruuj trójkąt, w którym jeden z boków ma długość a, wysokość opuszczona na ten bok ma długość h, a jeden z kątów leżących przy boku a jest równy a.

46. Punkt P jest środkiem narysowanego równoległoboku. Uzasadnij, że kąt a jest kątem prostym.

47. Zaznaczony trójkąt ABO ma pole równe 3cm2. Jakie jest pole równoległoboku ABCD?

48.  Udowodnij, że w trójkącie równoramiennym dwusieczne kątów przy podstawie są równe.

49.  Udowodnij, że w trójkącie równoramiennym środkowe ramion są równe.

50.  Udowodnij, że w trójkącie równoramiennym wysokości opuszczone na ramiona są równe.

51. W trójkącie równoramiennym połączono środki boków. Wykaż, że powstał trójkąt równoramienny.

52. Na podstawie AB trójkąta równoramiennego ABC obrano takie punkty K i L, że AK=LB.                                                                                                                                                       Uzasadnij, że CK = LC.

 

53. Na jednym ramieniu kąta o wierzchołku O obrano punkty A i B. Na drugim ramieniu    obrano punkty A1 i B1 tak, że OA = OA1 i OB = OB1. Uzasadnij, że AB1 = BA1 oraz, że punkt D przecięcia odcinków AB1 i BA1 leży na dwusiecznej danego kąta.

54.  Udowodnij, że jeżeli w trójkącie ABC kąty przy wierzchołkach A i B są równe, to          AC = BC.

55. Udowodnij, że jeżeli przekątne czworokąta są równe, przecinają się pod kątem prostym w punkcie, który jest ich wspólnym środkiem, to czworokąt ten jest kwadratem. Pokaż na przykładach, że opuszczenie któregokolwiek z tych warunków nie gwarantuje otrzymania kwadratu.

56. Wykaż, że kąt ostry wyznaczony przez przekątne prostokąta jest dwa razy większy od kąta, który tworzy przekątna z dłuższym bokiem prostokąta.

57.  W trójkącie jeden kąt jest prosty, jeden jest równy a. Oblicz miarę kąta między wysokością, a środkową wychodzącymi z wierzchołka kąta prostego w tym trójkącie.

58.  Uzasadnij, że dwusieczne kątów leżących przy tym samym ramieniu trapezu przecinają się pod kątem prostym.

59.  Na prostokątnej działce o wymiarach 20m i 26m biegnie wokół ogrodzenia ścieżka o szerokości 0,5m, ponadto są dwie ścieżki łączące środki przeciwległych boków mające również szerokość 0,5m. Poza ścieżkami stoi na działce altana o wymiarach 2,25m i 1,8m.Oblicz ile arów ma część uprawna tej działki.

60.  Punkty A = (-1,1), B = (7,1) i C = (2,3) są wierzchołkami trójkąta. Znajdź punkt D, taki że trójkąty ABC i ABD są przystające i C D (rozpatrz wszystkie przypadki).

61.  Zapisz nierówności, jakie spełniają współrzędne x i y punktów należących do narysowanego obok prostokąta?

62.  Wysokości trójkąta prostokątnego mają długości 60cm, 65cm i 156cm. Oblicz pole tego trójkąta.

63.  Jaki kąt tworzą wskazówki zegara o godzinie 1130, a jaki o godzinie 815.

64.  Narysuj okrąg o promieniu 3cm. Skonstruuj trójkąt prostokątny, którego przeciwprostokątna ma długość 6cm, a wysokość opuszczona na tę przeciwprostokątną jest równa 2,5cm.

65.  Narysuj kwadrat o boku 4cm i taką prostą k, aby pole figury złożonej z tego kwadratu i jego odbicia symetrycznego względem prostej k było równe 24cm2.

66.  Punkt P leży wewnątrz trójkąta ABC. Punkty P1, P2 i P3 są symetryczne do punktu P względem prostych AB, BC i AC. Wykaż, że pole wielokąta AP1BP2CP3 jest dwa razy większe od pola trójkąta ABC.

67.  Trójkąt ostrokąty ABC ma obwód d. Jaki obwód ma wielokąt zbudowany z trójkąta ABC oraz jego odbić symetrycznych względem prostych AB, AC i BC?

68.  Dany jest odcinek a oraz kąt ostry. Jak znaleźć wewnątrz tego kąta punkt, którego odległość od obu ramion kąta jest równa a?

69.  Punkty A= (-1,1), B = (-1,-3) i C = (5,-3) leżą na jednym okręgu. Jakie współrzędne ma środek tego okręgu?

70.  W trójkącie ABC dwusieczne kątów przy wierzchołkach A i B przecinają się w punkcie O. Przez punkt O prowadzimy proste równoległe do boków AC i BC, przecinające bok AB w punktach D i E. Uzasadnij, że obwód trójkąta DEO jest równy długości boku AB.

71.  W równoległoboku, który nie jest rombem, poprowadzono dwusieczne wszystkich kątów wewnętrznych. Uzasadnij, że czworokąt, którego wierzchołkami są punkty przecięcia tych dwusiecznych, jest prostokątem.

72.  W trójkącie prostokątnym przyprostokątne mają długości 15cm i 20cm.na krótszej przyprostokątnej jako na średnicy zbudowano okrąg. Oblicz długości odcinków na jakie ten okrąg podzielił przeciwprostokątną.

73.  W równoległoboku krótsza przekątna o długości 2 cm jest prostopadła do krótszego boku.
  Pole równoległoboku jest równe 8 cm2.Oblicz:

a)      obwód równoległoboku,

b)      wysokość opuszczoną na dłuższy bok.

74.  Oblicz pole trapezu, którego boki równoległe mają długości 16cm i 44cm, a nierównoległe 17cm i 25cm.


                                                                                                                                   Opracowała

mgr Grażyna Musielak

Powrót